Table of Contents
Farbwiedergabe
Der allgemeine Farbwiedergabewert $R_\mathrm{a}$ sagt aus, wie “echt” die Farben von Gegenständen für das menschliche Auge aussehen, wenn sie von einer Lampe beleuchtet werden. Der maximal erreichbare Farbwiedergabewert liegt bei 100, die Bewertung ist:
| Farbwiedergabeindex | Farbwiedergabestufe | Bewertung nach DIN |
|---|---|---|
| 90-100 | 1A | sehr hoch |
| 80-90 | 1B | sehr hoch |
| 70-80 | 2A | hoch |
| 60-70 | 2B | hoch |
| 40-60 | 3 | mittel |
| 20-40 | 4 | gering |
Für die Büro- oder Arbeitsplatzbeleuchtung werden nach DIN 5035 mindestens Farbwiedergabestufe 2A empfohlen, für Krankenhäuser und Speiseräume mindestens 1B, für besonders anspruchsvolle Aufgaben (z.B. Zahnarzt) 1A.
Berechnung des Farbwiedergabeindex
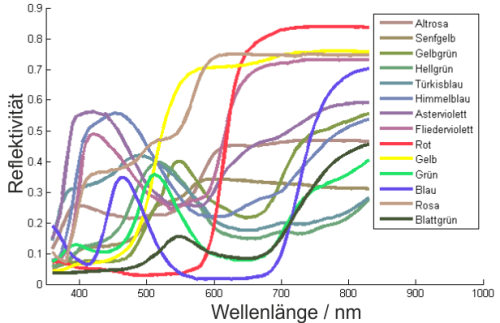
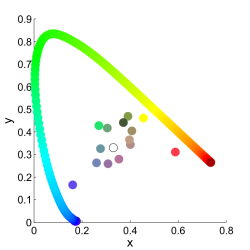
Zur Bestimmung des (Norm-)Farbwiedergabewerts einer Lichtquelle $K$ werden acht Testfarben, die in DIN 6169 definiert sind, mit der Lampe beleuchtet, und gemessen wie stark jede einzelne dieser Farben, im Vergleich zur Beleuchtung mit einer Bezugslichtquelle, auf der CIE-Farbkarte verschoben ist. Die Bestimmungen in DIN 6169 sind identisch zu denen in der CIE-Publikation. Es gibt keinen Unterschied zwischen dem “deutschen” Farbwiedergabeindex (Ra und dem englischen Colour Rendering Index (CRI). Insgesamt stehen in beiden Fällen nicht nur acht sondern 14 Testfarben zur Verfügung, wenn eine detailliertere Berechnung erwünscht ist. Diese werden aber meist separat angegeben, d.h. Ra als Mittelwert über R1 bis R8 und zusätzlich R9 als Farbwiedergabeindex für sattes Rot.
Um die Bezugslichtquelle zu finden, muss zuerst die Farbtemperatur der Lichtquelle $K$ bestimmt werden. Der Farbort der Lichtquelle $(x_K,x_K)$, darf dabei maximal um einen Abstand 5,4×10-3 im uv-Farbraum vom Planckschen Kurvenzug abweichen. Ist er weiter vom Planckschen Kurvenzug entfernt ist eine Berechnung des Farbwiedergabeindex nicht möglich.
Anhand der Farbtemperatur wird dann die Bezugslichtquelle gewählt. Liegt die Farbtemperatur unterhalb von 5'000 K ist die Bezugslichtquelle ein Planckscher Strahler mit der selben Farbtemperatur. Wenn die Farbtemperatur über 5'000 K ist, wird eine Phase des Tageslichts verwendet, die die selbe Farbtemperatur hat. Dazu wird aus der Serie der CIE-Normlichtarten “D” ein Spektrum mit der passenden Farbtemperatur gewählt [787Judd, D. B., MacAdam, D. L., Wyszecki, G., Budde, H. W., Condit, H. R., & Henderson, S. T., et al. (1964). Spectral distribution of typical daylight as a function of correlated color temperature. J. Opt. Soc. Am. 54(8), 1031–1040.]. Dazu hat die CIE die Spektren D65, ID65, ID50, 50, D55 und D75 definiert. Falls hier kein passendes Spektrum vorhanden ist, kann aus der Farbtemperatur $T_C$ ein Spektrum berechnet werden:
$$S(\lambda) = S_0(\lambda) + \frac{−1.3515 − 1.7703x_D + 5.9114y_D}{0.0241 + 0.2562x_D − 0.7341y_D}S_1(\lambda) + \frac{0.0300 − 31.4424x_D + 30.0717y_D}{0.0241 + 0.2562x_D − 0.7341y_D}S_2(\lambda)$$
mit $x_D = \frac{−4.6070\times 10^9}{T_C^3} + \frac{2.9678\times 10^6}{T_C^2} + \frac{0.09911\times 10^3}{T_C} + 0.244063$ (für 4000 K $< T_C <$7000 K) und $y_D = −3.000x_D^2 + 2.870x_D − 0.275$. [1212Hunt, R. W. G., & Pointer, M. R. (2011). Measuring colour. John Wiley & Sons, Ltd.]
Anschließend werden die Farborte von acht (oder 14) Testfarben bei Beleuchtung mit der Lichtquelle $K$ und Beleuchtung mit der Bezugslichtquelle $R$ bestimmt. Die Farben werden dabei mit $i=1\ldots 8$ durchnummeriert. Die Farborte werden als $(X_{ir},Y_{ir},Z_{ir})$ (für die Bezugslichtquelle) und $(X_{ik},Y_{ik},Z_{ik})$ für die Lichtquelle bezeichnet.
Die Farborte werden in den uv-Farbraum transformiert: $(u_{ir}, v_{ir})$, $(u_{ik}, v_{ik})$. Da die Farborte der Lichtquelle $K$ und der Bezugslichtquelle $R$ nicht identisch sind, sondern nur ihre ähnlichsten Farbtemperaturen gleich sind, muss die chromatische Adaption des Auges an die Farbe des Lichts berücksichtigt werden. Dazu werden die Farborte $(u_{ir}, v_{ir})$ zu $(u'_{ir}, v'_{ir})$ transformiert. Diese Transformation ist auch als van Kries-Transformation bekannt.
Zuletzt werden diese Koordinaten in den CIE 1964 Farbraum transformiert und in diesem Koordinatensystem wird der Abstand $\Delta E_i$ für jede Farben bestimmt. Der Abstand entspricht dem Farbwiedergabeindex für diese Farbe $R_i = 100 - 4,6\Delta E_i$. Der allgemeine Farbwiedergabeindex ist der Mittelwert für alle acht Farben $R_{\mathrm{a}} = \frac{1}{8}\sum_{i=1}^8 100 - 4,6\Delta E_i = \frac{1}{8}\sum_{i=1}^8 R_i$
Farbwiedergabe und "Ähnlichkeit zum Sonnenspektrum"
Häufig liest man
Der »Ra-Wert« sagt aus wie natürlich das Spektrum der Lampe ist. Eine hohe Ziffer, zum Beispiel 8xx (=80 Ra) oder 9xx (=90 Ra), besagt, dass die Zusammensetzung des Lichtes dem Sonnenlicht sehr ähnlich ist.
Diese Aussage ist falsch! Aus der Berechnung der Farbwiedergabeindex sieht man direkt, dass das Spektrum der Lampe zu keiner Zeit mit dem Sonnenlicht verglichen wird.
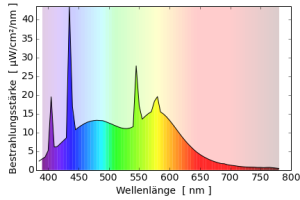
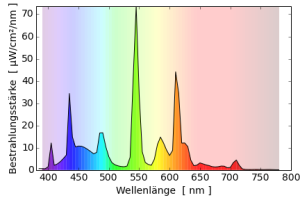
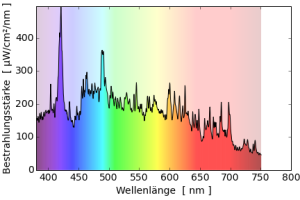
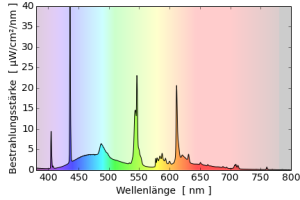
Deutlich wird das vielleicht an den Spektren der Zweibanden- und Dreibandenleuchtstofflampen: Obwohl das Spektrum der Zweibandenleuchtstofflampen gleichmäßiger ist, hat diese Lampe den deutlich schlechteren Farbwiedergabeindex.
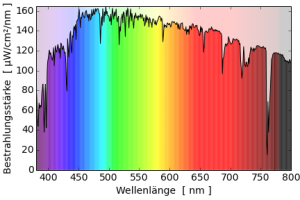
Andererseits können zwei Lampen mit gleicher Farbwiedergabe sehr unterschiedlich vom Sonnenspektrum abweichen: Obwohl die Vollspektrumleuchtstofflampe und die hqi-Lampe beide einen Farbwiedergabeindex von 96 haben, ist nur das Spektrum der hqi-Lampe sonnenähnlich. Das Spektrum der Leuchtstofflampe weist große Lücken um 550nm und 400nm auf und hat extrem hohe Quecksilberlinien.
Farbwiedergabe und Reptilien
Da Reptilien ein anderes Sehvermögen haben als der Mensch, ist der Farbwiedergabenindex bei der Auswahl einer Lampe nicht hilfreich. Bei genauer Prüfung des Spektrums kann eine Lampe mit schlechterem Farbwiedergabewert geeigneter sein.
Literatur
[787] Judd, D. B., MacAdam, D. L., Wyszecki, G., Budde, H. W., Condit, H. R., & Henderson, S. T., et al. (1964). Spectral distribution of typical daylight as a function of correlated color temperature. J. Opt. Soc. Am. 54(8), 1031–1040.
[1212] Hunt, R. W. G., & Pointer, M. R. (2011). Measuring colour. John Wiley & Sons, Ltd.
[603] Farbwiedergabe: Farbwiedergabe-eigenschaften von lichtquellen in der beleuchtungstechnik. (1976). DIN 6169-2Deutsches Institut für Normung e.V.
Discussion