- Wirkungsspektrum der betrachteten Wirkung [UVB, UVA, UV-Index, Vitamin D …]: $W(\lambda)$, einheitenlos, meist normiert auf max($W(\lambda)$)=1)
- Spektrale Empfindlichkeit des Messgerätes: $A(\lambda)$, einheitenlos, meist normiert auf max($A(\lambda)$)=1)
- spektrale Bestrahlungsstärke der Lichtquelle: $E_\lambda(\lambda)$, Einheit µW/cm²/nm
- spektrale Bestrahlungsstärke der Kalibrierungs-Lichtquelle: $E^\mathrm{Kalibr.}_\lambda(\lambda)$, Einheit µW/cm²/nm
- Korrekturfaktor: $a$
- Kalbrierungsfaktor: $K$
Table of Contents
UV-Radiometer (Breitbandmessgeräte)

UV-Radiometer gehören zu den beliebtesten UV-Messgeräten, da sie zu einem erschwinglichen Preis (ab ca. 150€) erhältlich sind. Sie zeichnen sich durch eine hohe Reproduzierbarkeit der Messergebnisse, einem hohen Signal zu Rausch Verhältnis und eine sehr einfache Handhabung aus.
Alle diese Vorteile, die UV-Radiometer im Vergleich zu Spektrometern besitzen, machen Sie zu beliebten Messgeräten für Reptilienhalter. Die Interpretation der Messwerte ist jedoch vergleichsweise kompliziert: UV-Radiometer messen die Bestrahlungsstärke gewichtet mit ihrem eigenen Empfindlichkeitsspektrum, das nicht mit der meist gleichnamigen Bezeichnung des Messgeräts überein stimmt. Messwerte verschiedener Lampen oder verschiedener Messgeräte sind daher grundsätzlich nicht vergleichbar. So kann eine Lampe, die einen geringeren Messwert an einem UVB-Messgerät als eine andere Lampe hat, dennoch eine höhere UVB-Bestrahlungsstärke haben.
Ohne Kenntnis
- des Spektrums der Lichtquelle
- des Empfindlichkeitsspektrums des UV-Radiometers
- des Kalibrationsverfahrens des UV-Radiometers
- des Wirkungsspektrums der betrachteten Wirkung der Strahlung
hat der Einsatz eines Breitbandmessgeräts nur sehr begrenzte Aussagekraft.
Aufbau und Funktion eines UV-Radiometers
Hinweis zur Nomenklatur1)
Photodiode
Die Grundlage der üblichen UV-Radiometer ist eine Halbleiter-Photodiode. Der Strom, der durch eine solche Photodiode fließt ändert sich, wenn ein Photon (Licht-Teilchen) im Halbleiter absorbiert wird. Die Photodiode reagiert jedoch nicht auf jedes Photon gleich! Die Wellenlänge des Photons muss zur Bandlücke des Halbleiters passen. Für Messgeräte im sichtbaren Bereich wird meist ein Silizium-Halbleiter verwendet. Um die Bandlücke an eine UV-Messung anzupassen sind andere Halbleiter, beispielsweise SiC, GaN, Diamant oder GaAsP, nötig. Da die spektrale Empfindlichkeit der Photodiode meist noch nicht die gewünschte Form hat, kann sich durch Filter weiter eingeschränkt werden.
Im Quasi-Kurzschluss-Betrieb hängt die Stromstärke linear von der Anzahl der einfallenden Photonen ab. Photodioden sind daher hervorragend zur Messung der Bestrahlungsstärke geeignet.
Letztlich fasst man diese Effekte im der spektralen Empfindlichkeitsspektrum $A(\lambda)$ des Radiometers zusammen:
Als Formel ausgedrückt, ist das Stromsignal $S$ der Photodiode \[ S = \int\mathrm{d}\lambda E_\lambda(\lambda) = \Delta\lambda \cdot \sum_n E_\lambda (\lambda_n) \cdot A(\lambda_n) \] Diese Formel kann als Summe ($\sum_n$) oder als Integral ($\int$) geschrieben werden, und ist als Summe für mathematisch ungeübte Menschen wohl einfacher zu verstehen. Die Anweisung lautet: Bei jeder Wellenlänge $\lambda_n$ ($\lambda_n$ ist beispielsweise 280nm, 281nm, 282nm usw. in Schritten $\Delta\lambda=$1nm) wird die Bestrahlungsstärke des Lichts $E_\lambda(\lambda_n)$ gemessen und mit der spektralen Empfindlichkeit $A(\lambda_n)$ bei dieser Wellenlänge $\lambda_n$ multipliziert. Anschließend werden alle Werte addiert.
Beispiel
| $n$ | $\lambda_n$ | $E_\lambda(\lambda_n)$ | $A(\lambda_n)$ | $E_\lambda(\lambda_n)\cdot A(\lambda_n)$ |
|---|---|---|---|---|
| 1 | 280 nm | 0.002 µW/cm²/nm | 100 | 0.002 µW/cm²/nm |
| 2 | 285 nm | 0.001 µW/cm²/nm | 99 | 0.001 µW/cm²/nm |
| 3 | 290 nm | 0.035 µW/cm²/nm | 97 | 0.034 µW/cm²/nm |
| 4 | 295 nm | 0.049 µW/cm²/nm | 93 | 0.137 µW/cm²/nm |
| 5 | 300 nm | 0.529 µW/cm²/nm | 81 | 0.429 µW/cm²/nm |
| 6 | 305 nm | 1.829 µW/cm²/nm | 73 | 1.638 µW/cm²/nm |
| 7 | 310 nm | 5.477 µW/cm²/nm | 65 | 3.541 µW/cm²/nm |
| 8 | 315 nm | 13.442 µW/cm²/nm | 58 | 7.398 µW/cm²/nm |
| 9 | 320 nm | 13.627 µW/cm²/nm | 44 | 5.998 µW/cm²/nm |
| 10 | 325 nm | 17.569 µW/cm²/nm | 21 | 3.942 µW/cm²/nm |
| 11 | 330 nm | 25.637 µW/cm²/nm | 4 | 1.133 µW/cm²/nm |
| 12 | 335 nm | 32.354 µW/cm²/nm | 0 | 0.043 µW/cm²/nm |
| 13 | 340 nm | 41.639 µW/cm²/nm | 0 | 0.071 µW/cm²/nm |
| $\sum_n E_\lambda (\lambda_n) \cdot A(\lambda_n)$ | 24.36 µW/cm²/nm | |||
| $\Delta\lambda \cdot \sum_n E_\lambda (\lambda_n) \cdot A(\lambda_n)$ | 5 nm $\cdot$ 24.36 µW/cm²/nm = 121.8 µW/cm² | |||
Kosinuskorrektur
Wenn die Sonne schräg auf eine Fläche scheint, verringert sich die Intensität der Strahlung auf der Oberfläche. Sind zwischen Sonne und Oberflächennormale eine Winkel $\phi$, so kann die Fläche nur nur $I_0\cos\phi$ der maximalen Intensität absorbieren.
Messgeräte reagieren nicht immer richtig auf Licht aus verschiedenen Winkeln. Eine entsprechend dimensionierte Streuscheibe mit Abschattungsringen kann das korrigieren.
Kalibrierung
Die Stromstärke der Photodiode wird anschließend in der Elektronik des Messgeräts mit einem Kalibrierungsfaktor multipliziert damit das Ergebnis in einer sinnvollen Größe am Display angezeigt werden kann. Viele Messgeräte geben die effektive Bestrahlungsstärke in µW/cm² oder W/m² an. Andere Messgeräte verwenden z.B. den UV-Index oder die gebildete Vitamin D3 Menge (internationale Einheiten pro Minute) an. Die gewählte Einheit (µW/cm², UV-Index …) ist für die praktische Anwendung allerdings nahezu bedeutungslos da es sich lediglich um einen Faktor bei der Anzeige handelt der nichts damit zu tun hat, wie der Wert physikalisch entsteht.
Um diesen Kalibrierungsfaktor zu finden, braucht man eine Kalibrierungslampe. Diese Lampe wird sowohl mit dem Radiometer als auch einem Spektrometer gemessen und die beiden Ergebnisse verglichen. Der Kalibrierungsfaktor wird dann so gewählt, dass die beiden Ergebnisse exakt gleich sind.
Beispiel
| UVB Messwert Spektrometer | $\int\mathrm{d}\lambda W(\lambda)E^\text{kalibr.}_\lambda(\lambda)$ | 140 µW/cm² |
|---|---|---|
| Stromsignal UV-Radiometer | $\int\mathrm{d}\lambda A(\lambda)E^\text{kalibr.}_\lambda(\lambda)$ | 122 µW/cm² |
| Kalibrierungs-Faktor | $K$ | 140/121.8 = 1.147 |
Der Messwert des Radiometer für eine Lichtquelle $E_\lambda(\lambda)$ ist letztlich \[ M = K\cdot \int\mathrm{d}\lambda A(\lambda)E_\lambda(\lambda) \]
Kalibrierungsmethoden
Zur Kalibration gibt es drei Möglichkeiten: Verwendung einer Linienlichtquelle, Verwendung einer breitbandigen Lichtquelle oder Messung der Spektralen Empfindlichkeit des Messgeräts [120Kärhä, P. (2002). Calibration and intercomparison issues with broadband uv meters. UV News, 7, 29–34.].
Als Linienlichtquelle wird üblicherweise eine Quecksilberdampflampe (254 nm, 313 nm, 365 nm) verwendet. Um den korrekten Messwert zu bestimmen, kann die Lampe mit einem einfachen Powermeter gemessen werden. Diese Methode ist schnell, einfach und sehr gut reproduzierbar. Bei Kalibration mit einer Linienlichtquelle liefert die Messung Bestrahlungsstärke einer breitbandingen Lichtquelle oft einen zu kleinen Wert, die Messung einer Linienlichtquelle einen zu hohen Wert [119Gugg-Helminger, A., Dähn, W., & Fenk, S. (2002). Manufacturer’s view on uv meters with different action spectra. UV News, 7, 20–28.].
Für Anwendungen im medizinischen Bereich wird meist mit einer breitbandingen Lichtquelle kalibriert. Dazu muss die breitbandige Lichtquelle zusätzlich mit einem Spektrometer vermessen werden, um herauszufinden, welcher Wert der korrekte Messwert ist.
Die fundierteste aber aufwändigste Kalibrationsmethode ist die Ermittlung der spektralen Empfindlichkeitskurve des Messgeräts.
Robertson-Berger-Messgeräte
Anstelle einer Photodiode, die empfindlich im UV-Bereich ist, kann auch eine Photodiode für den sichtbaren Bereich zusammen mit einem Leuchtstoff, der UV-Strahlung in sichtbares Licht umwandelt verwendet werden. Ein solches Messgerät wurde in den 1950ern von Robertson in Australien entwickelt und von Berger in den USA modifiziert. Die prinzipiellen Betrachtungen gelten für beide Typen.
Korrekturfaktor / Systematische Fehler
Der Kalibrierungsfaktor ist so gewählt, dass das Radiometer bei der Kalibrierungslampe den selben Messwert anzeigt wie ein Spektrometer. Sobald jedoch die Lampe ein anderes Spektrum hat, als die Kalibrierungslampe, wird der Radiometer-Messwert sich von einem Spektrometer-Messwert stark unterschieden. Das liegt daran, dass in der obigen Summe das Spektrum der Lampe einen großen Einfluss hat.
Hierbei handelt es sich um einen systhematischen Fehler: Sobald das Spektrum der Lampe bekannt ist, ist er kein großes Problem, weil man einfach ausrechnen kann, welchen Messwert ein Radiometer für diese Lampe liefern sollte und welchen spektralen Messwert man erwarten würde und einen entsprechenden Korrekturfaktor $a$ berechnet [38Gugg-Helminger, A., Dähn, W., Fenk, S., & Angelo, B. 2004, October 1 Broadband and spectral measurement instrumentation for photobiological hazard evaluation. Unpublished paper presented at CIE Expert Symposium on Light and Health.; 119Gugg-Helminger, A., Dähn, W., & Fenk, S. (2002). Manufacturer’s view on uv meters with different action spectra. UV News, 7, 20–28.]. Anschließend multipliziert man den Radiometer-Messwert einfach mit diesem Korrekturfaktor und die Messwerte sind genauso perfekt als wenn man von Anfang an ein Spektrometer verwendet hätte allerdings ohne die umständliche Handhabung eines Spektrometers (lange Integrationszeit, nicht sehr beweglich, braucht viel Platz).
\[ a = \frac{ \int\mathrm{d}\lambda E^\mathrm{kalibr.}_\lambda(\lambda)\cdot W(\lambda) }{ \int\mathrm{d}\lambda E^\mathrm{kalibr.}_\lambda(\lambda)\cdot A(\lambda) } \frac{ \int\mathrm{d}\lambda E_\lambda(\lambda)\cdot A(\lambda) }{ \int\mathrm{d}\lambda E_\lambda(\lambda)\cdot W(\lambda) } = \frac{ K \int\mathrm{d}\lambda E_\lambda(\lambda)\cdot A(\lambda) }{ \int\mathrm{d}\lambda E_\lambda(\lambda)\cdot W(\lambda) } \]
Man kann sogar einen Schritt weiter gehen und einen Korrekturfaktor für diese Lampe und dieses Radiomter für ein anderes Wirkspektrum berechnen. Sobald man diesen Korrekturfaktor hat, kann man ein UVB-Radiometer theoretisch auch verwenden um (für diese spezielle Lampe!) den UV-Index oder die effektive Bestrahlungsstärke für Vitamin D zu messen.
Beispiel:
| Breitbandmessgerät | Spektrometer | Korrekturfaktor | |
|---|---|---|---|
| UVB: | 89,6 µW/cm² | 98 µW/cm² | 98/89,6 = 1,09 |
| Vitamin D: | - | 14 µW/cm² | 14/89,6 = 0,156 |
| Breitband-Messwert | korrigiert für UVB ( x 1,09) | korrigiert für Vitamin D ( x 0,156 ) |
|---|---|---|
| 50 µW/cm² | 54,5 µW/cm² | 7,8 µW/cm² |
| 100 µW/cm² | 109 µW/cm² | 15,6 µW/cm² |
| 150 µW/cm² | 163,5 µW/cm² | 23,4 µW/cm² |
| 200 µW/cm² | 218 µW/cm² | 31,2 µW/cm² |
| 300 µW/cm² | 327 µW/cm² | 46,8 µW/cm² |
Falls sich herausstellt, dass der Korrekturfaktor gleich 1 ist, hätte man sich die Mühe den Korrekturfaktor auszurechnen auch sparen können, denn wenn man einen Wert mit 1 multipliziert, ändert er sich nicht.
Der Korrekturfaktor ist in zwei Fällen sehr nahe bei 1 (und das bedeutet: man muss ihn nicht berechnen sondern kann das Radiometer direkt verwenden):
- Der Korrekturfaktor ist nahe bei 1, wenn das Spektrum der Lichtquelle und das Spektrum der Kalibrierungslichtquelle ähnlich, in dem Bereich in dem das Radiometer arbeitet, sind.
- Der Korrekturfaktor ist nahe bei 1, wenn die spektrale Empfindlichkeit des Radiometers und die Wirkungsfunktion (UVB, VitaminD, UV-Index) ähnlich sind.
Der Korrekturfaktur muss für jedes Messgerät ($A(\lambda)$ mit Kalibrierung $K$) und jede gewünschte Anwendung (Wirkungsspektrum $W(\lambda)$ und Lampe $E_\lambda(\lambda)$) bestimmt werden. Pauschale Aussagen über den Fehler eines Breitbandmessgeräts sind unseriös.
Will man die Abhängigkeit von der konkreten Lampe reduzieren, bietet sich, der “Integral characterisation factor” $f_1'$ an [112Characterizing the performance of integral measuring uv-meters. (2000). UV News, 6, A-1–AA-36.] 2) : \[ f_1' = \frac{ \int\mathrm{d}\lambda \left| W(\lambda)-K A(\lambda)\right| }{ \int\mathrm{d}W(\lambda) } \]
Literatur zu Korrekturfaktoren
| Quelle | Lichtquelle | Messbereich | Abweichung Breitband/Spektrometer | spektraler Korrekturfaktor | |
|---|---|---|---|---|---|
| 121 | Xenon+Filter | UV-Index | 1/1.85 - 2.22 | verschiedene Handelsübliche UV-Messgeräte | |
| 121 | Xenon+Filter | dUVA | 1/1.3 - 5.51 | verschiedene Handelsübliche UV-Messgeräte | |
| 320 | VitaminD-Bildung | ||||
| 474 | VitaminD-Bildung | ||||
| 38 | UV-Lampen | UV-Index | 1/2-5 - 1.6 | ||
| 38 | Sonne | UV-Index | 1.2 - 2.2 | ||
| 277;667 | Xenon+Filter | UVA | 1.18 - 1.42 | ||
| 277;667 | Xenon+Filter | UVB | 1/25 - 16 | ||
| 676 | Sonne (132 Spektren) | UV-Index | R²=99.8% | ohne Korrekturfaktoren | |
| 676 | Sonne (132 Spektren) | UV-Index | R²= 99.98% | nach Korrektur für SZA und Ozon | |
| 119 | UV-Lampen,Sonne | UV-Index | 0.7-6.3 |
Siehe auch [668Hoffmann, H., & Kirschner, A. (2010). Leserbrief. Elaphe N.F. 4, 76.]
Genauigkeit / Statistische Fehler
Breitbandradiometer gelten generell als robuster und stabiler als Spektroradiometer [678Webb, A. R. (2000). Standardisation of data from ultraviolet radiation detectors. Radiation Protection Dosimetry, 91(1-3), 123–128.], dennoch ist ihre Genauigkeit durch verschiedene statistische und systematische Fehler begrenzt [112Characterizing the performance of integral measuring uv-meters. (2000). UV News, 6, A-1–AA-36.][280Larason, T. C. (2001). Avoiding errors in uv radiation measurements. Photonics Spectra,].
- Linearität: Photodioden zeichnen sich durch eine hohe Linearität ab, dennoch kann das Messgerät nichtlinear auf die Bestrahlungsstärke reagieren, d.h. trotz doppelter Bestrahlungsstärke nicht den doppelten Messwert anzeigen
Bei 121 variierte der Messwert zwischen niedriger und hoher Bestrahlungsstärke um einen Faktor 4. - Temperaturabhängigkeit: Sowohl die spektrale als auch die absolute Empfindlichkeit des Messgeräts kann Temperaturabhängig sein, so dass ein Messgerät das durch die Wärmestrahlung der Lampe aufgeheizt wird, veränderte Werte liefert (→172)
- Richtungs- und Verteilungsabhängigkeit: Bei inhomogener Lichtverteilung über die Fläche und das Gesichtsfeld des Sensors kann es zur Verfälschung des Messwerts kommen (→117,280)
- Modulation: Bei Lampen deren Strahlung zeitlich schwankt (z.B. Mischlichtlampen) kann das den Messwert beeinflussen
- Rauschen: Insbesondere wenn sehr kleine Messwerte gemessen werden sollen, spielt das statistische Dunkelsignal der Photodiode eine Rolle. Das Rauschen von UV Breitbandmessgeräten ist - vor allem im Vergleich zu günstigen Spektrometern - sehr gering.
- Alterung: Durch den Einfluss der UV-Strahlung altern Breitbandmessgeräte und müssen regelmäßig nachkalibriert werden.
- Out of Band Response: Manche Messgeräte reagieren auch außerhalb ihrer angebenen eigentlichen Empfindlichkeit auf Strahlung. Bei einigen UVC-Messgeräten ist bekannt, dass sie auch auf UVA-Strahlung reagieren. Hierbei handelt es sich eigentlich um eine Systematischen Fehler der in den Korrekturfaktor integriert werden kann, jedoch ist dieser Out-of-band-Response häufig im Datenblatt nicht angegeben.
Neben diesen Fehlern hat die spektrale Empfindlichkeit des Messgeräts im Vergleich zur Größe die gemessen werden soll, einen größeren Einfluss auf den systematischen Fehler bei der Interpretation des Messwerts.
Verhältnis zweier Breitbandmessgeräte
Der Messwert eines einzelnen Breitbandmessgeräts $M_1=K\int\mathrm{d}\lambda E_\lambda(\lambda) A(\lambda)$ enthält kaum Information über das Spektrum der Lichtquelle. So lässt sich allein durch Änderung des Abstands bei jeder UV-Lampe der selbe Messwert erzeugen.
Durch den Vergleich der Werte zweier Messgeräte mit unterschiedlicher Empfindlichkeit lässt sich diese Information erhöhen. Das Verhältnis der Messwerte ist abhängig von der Form (aber nicht der Intensität!) des Lampenspektrums und der Empfindlichkeitsspektren der Messgeräte.
\[ \frac{M_1}{M_2} = \frac{ K_1\int\mathrm{d}\lambda E_\lambda(\lambda) A_1(\lambda) }{ K_2\int\mathrm{d}\lambda E_\lambda(\lambda) A_2(\lambda) } = f\left(E_\lambda^\mathrm{norm.}(\lambda),A_1(\lambda),A_2(\lambda)\right) \]
Wenn die normierten Empfindlichkeitsspektren der beiden Messgeräte eine Differenz $D(\lambda)$ hat, lässt sich das noch genauer schreiben als \[ \begin{eqnarray} A_1(\lambda) &=& A_2(\lambda) + D(\lambda) \\\\ \frac{M_1}{M_2} &=& \frac{ K_1\int\mathrm{d}\lambda E_\lambda(\lambda) A_2(\lambda) + K_1\int\mathrm{d}\lambda E_\lambda(\lambda) D(\lambda) }{ K_2\int\mathrm{d}\lambda E_\lambda(\lambda) A_2(\lambda) } \\\\ &=& \frac{K_1}{K_2} + \frac{ K_1\int\mathrm{d}\lambda E_\lambda(\lambda) D(\lambda) }{ M_2 } \end{eqnarray} \]
Dieser Wert kann aus Messwerten bei verschiedenen Abständen von der Lampe ermittelt werden, wenn das Spektrum abstandsunabhängig ist und die Kosinuskorrektur beider Messgeräte hinreichend ähnlich ist. Zur statistischen Analyse der Daten stehen verschiedene Methoden der Regressionsanalyse zur Verfügung.
Solarmeter
Die Firma Solartech stellt verschiedene Messgeräte her, die aufgrund ihres Preis-Leistungsverhältnisses in der Terraristik sehr beliebt sind. Beim Hersteller sind Kalibrationsspektrum und spektrale Empfindlichkeit der Messgeräte erhältlich. Die Messgeräte sind mit einer Leuchtstofflampe mit sonnenähnlichem Spektrum kalibriert.
- Solarmeter 6.2 (UVB)
- Einheit UVB µW/cm²
- Übereinstimmung mit $W(\lambda)$=Vitamin D
$1-\frac{1}{2}\int\limits_{280nm}^{400nm}\mathrm{d}\lambda \left|\overline{A}(\lambda)-\overline{W}(\lambda)\right| = $75%
(Einer Interpretation dieser Formel durch JBL709 schließe ich mich explizit nicht an)
- Solarmeter 6.5 (UV index)
- Einheit UVI-Index (UVI=1 entspricht 2.5µW/cm²)
- Übereinstimmung mit $W(\lambda)$=Vitamin D
$1-\frac{1}{2}\int\limits_{280nm}^{400nm}\mathrm{d}\lambda \left|\overline{A}(\lambda)-\overline{W}(\lambda)\right| = $90%
$1-\frac{1}{2}\int\limits_{290nm}^{400nm}\mathrm{d}\lambda \left|\overline{A}(\lambda)-\overline{W}(\lambda)\right| = $96% - Aufgrund der hohen Übereinstimmung mit der VitaminD-Kurve nach DIN/CIE und weil das Messgerät auf Strahlung oberhalb von 315nm nur mit <4%, und oberhalb 320nm nur mit <1% reagiert ist dieses Messgerät gut geeignet, die VitaminD-Wirksamkeit einer Lampe abzuschätzen.
- Dieses Messgerät ist sowohl mit einem SiC-Sensor als auch mit einem AlGaN-Sensor erhältlich. Lediglich der SiC-Sensor ist für kurzwellige Strahlung empfindlich und daher für unsere Zwecke vorzuziehen. Die Messwerte des Solarmeter 6.5 (UV-Index) und das Solarmeter 6.4 (VitaminD) mit SiC-Sensor können direkt in einander umgerechnet werden, da die Messgeräte bis auf die Anzeige identisch sind: SM6.4 = 7.14 · SM6.5
- Solarmeter 8.0 (UVC)
- Einheit UVC µW/cm²
Das Messgerät ist für langwellige Strahlung nicht völlig blind. Bei Lampen mit sehr intensiver sichtbarer und UVA-Strahlung kann das Solarmeter einen Wert anzeigen, obwohl die Lampe kein UVC abstrahlt. Mit einem Schott WG295-Filter, der Strahlung unterhalb von 295nm blockiert kann man kontrollieren, ob der Solarmeter 8.0-Messwert teilweise durch UVA oder sichtbare Strahlung verursacht wird.
Interpretation der Messwerte
Der selbe Messwert des Solarmeter 6.2 oder 6.5 kann - je nach Spektrum der Lampe - eine ganz andere Bedeutung für die Verbrennungsgefahr durch UV-Strahlung und die Eignung zur Vitamin D Synthese haben (Korrekturfaktoren, siehe oben). Die beiden folgenden Tabellen listen Werte für einige typische Lampen auf.
| Lichtquelle | Solarmeter | effektive Bestrahlungsstärke (µw/cm²) | UVB (µw/cm²) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 6.2 | 6.5 | 6.2:6.5 | Vitamin D | Erythem | Photo keratitis | DNA Schädigung | EU | US | |
| Sonne, 20° | 150 | 2.2 | 100:1.5 | 5.7 | 4.9 | 28 | 0.011 | 44 | 89 |
| Sonne, 40° | 150 | 3.5 | 100:2.4 | 11 | 6.7 | 3.3 | 0.12 | 61 | 100 |
| Sonne, 60° | 150 | 4.6 | 100:3.1 | 14 | 8.3 | 4.5 | 0.19 | 67 | 110 |
| Sonne, 85° | 150 | 5 | 100:3.3 | 16 | 9.1 | 4.9 | 0.23 | 69 | 110 |
| MLR | 150 | 2.9 | 100:1.9 | 11 | 5.9 | 5.9 | 0.047 | 140 | 150 |
| MLR | 150 | 6 | 100:4 | 20 | 16 | 9.9 | 4.3 | 120 | 140 |
| MLR | 150 | 11 | 100:7.2 | 38 | 24 | 16 | 2.2 | 130 | 140 |
| UVB-313 | 150 | 18 | 100:11.8 | 55 | 45 | 28 | 7.5 | 100 | 130 |
| UVA-340 | 150 | 4.2 | 100:2.8 | 14 | 8 | 4.7 | 0.2 | 59 | 110 |
| Lichtquelle | Solarmeter | effektive Bestrahlungsstärke (µw/cm²) | UVB (µw/cm²) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 6.2 | 6.5 | 6.2:6.5 | Vitamin D | Erythem | Photo keratitis | DNA Schädigung | EU | US | |
| Sonne, 20° | 270 | 4 | 100:1.5 | 10 | 8.9 | 52 | 0.02 | 79 | 160 |
| Sonne, 40° | 170 | 4 | 100:2.4 | 12 | 7.5 | 3.8 | 0.13 | 69 | 110 |
| Sonne, 60° | 130 | 4 | 100:3.1 | 13 | 7.2 | 3.9 | 0.17 | 58 | 94 |
| Sonne, 85° | 120 | 4 | 100:3.3 | 13 | 7.3 | 3.9 | 0.19 | 55 | 86 |
| MLR | 210 | 4 | 100:1.9 | 15 | 8 | 8 | 0.065 | 190 | 210 |
| MLR | 99 | 4 | 100:4 | 13 | 11 | 6.5 | 2.8 | 78 | 92 |
| MLR | 55 | 4 | 100:7.2 | 14 | 8.9 | 5.9 | 0.81 | 49 | 52 |
| UVB-313 | 34 | 4 | 100:11.8 | 12 | 10 | 6.2 | 1.7 | 23 | 28 |
| UVA-340 | 140 | 4 | 100:2.8 | 13 | 7.6 | 4.5 | 0.19 | 56 | 100 |
Verhältnis Solarmeter 6.5 und Solarmeter 6.2
In den letzten Jahren hat es sich etabliert, das Verhältnis zwischen Solarmeter 6.5 und Solarmeter 6.2 zur Bewertung von UV Lampen heranzuziehen.
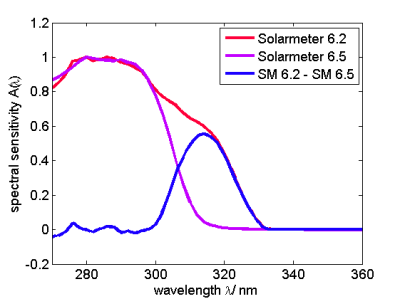
Die spektrale Empfindlichkeit des Solarmeter 6.5 ($A_{6.5}(\lambda)$) und Solarmeter 6.2 ($A_{6.2}(\lambda)$) und die Differenz der beiden Empfindlichkeiten $D(\lambda)=A_{6.2}(\lambda)-A_{6.5}(\lambda)$ sind im folgenden Bild dargestellt:
Das Verhältnis der Messwerte \[ \frac{M_{6.2}}{M_{6.5}} = \frac{K_{6.2}}{K_{6.5}} + \frac{ K_{6.2}\int\mathrm{d}\lambda E_\lambda(\lambda) D(\lambda) }{ M_{6.5} } \] hangt also stark davon ab, wie die Lampe ($E_\lambda(\lambda)$) mit $D(\lambda)$ überlappt. Für eine Lampe die viel Strahlung im Bereich 310-320nm hat, der für die Vitamin D Synthese weniger wirksam ist, ist das Verhältnis $M_{6.2}/M_{6.5}$ groß. Wenn dieser Bereich weniger Intensität enthält und die Strahlung stärker auf den Bereich unterhalb von 310nm konzentriert ist, ist das Verhältnis $M_{6.2}/M_{6.5}$ klein.
Der Vergleich beider Messwerte enthält also eine Information darüber, ob die UVB-Strahlung mehr im kurzwelligen Bereich <310nm oder im langwelligen Bereich >310nm konzentriert ist. 
Da jedoch die meisten Lampen sehr typische Spektren haben (da meist gleiche Gläser und Leuchtstoffe verwendet werden) ist diese Abschätzung zwar ungenauer als eine Messung mit Spektrometer, kann aber dennoch eine nützliche Abschätzung geben, wie der Messwert eines Messgeräts interpretiert werden muss. Bei typischen Lampenspektren (siehe oben) kann aus dem Verhältnis auf die Form des Spektrums (z.B. verwendete Leuchtstoffe) geschlossen werden.
Bei manchem Lamenspektren kann das Verhältnis (ebenso wie der reine Messwert) sehr irreführend sein: So haben UVA340-Röhren, die gut geeignet zur Vitamin D Synthese sind und manche Schwarzlichtröhren, deren Spektrum kaum zur Vitamin D Synthese geeignet ist, ein Verhältnis von etwa $\frac{M_{6.2}}{M_{6.5}}=55$. Eine schmalbandige UV-Leuchtstofflampe mit Emission um 305±5nm (mir ist eine solche Lampe nicht bekannt) würde zu einem sehr geringen $\frac{M_{6.2}}{M_{6.5}}$-Verhältnis führen obwohl keine Strahlung unterhalb 300nm vorhanden ist.
Für die oben aufgelisteten typischen Lampenspektren gilt:
| $\frac{M_{6.2}}{M_{6.5}}$ | $\frac{M_{6.5}}{M_{6.2}}$ | Beurteilung |
| > 60 | <0.016 | langwellige UVB-Strahlung: voraussichtlich geringe Vitamin-D-Bestrahlungsstärke und geringe Verbrennungs-Bestrahlungsstärke typisch für normale Leuchtstofflampen und Vollspektrumlampen |
| 50-60 | 0.016 - 0.02 | natürliches Sonnenlicht |
| < 50 | > 0.025 | kurzwelliger Schwerpunkt der UVB-Strahlung: voraussichtlich erhöhte Vitamin-D-Bestrahlungsstärke und Verbrennungs-Bestrahlungsstärke typisch für viele Zoohandels-UV-Lampen |
| < 20 | > 0.05 | sehr kurzwelliger Schwerpunkt der UVB-Strahlung: voraussichtlich hohe Vitamin-D-Bestrahlungsstärke und hohe Verbrennungs-Bestrahlungsstärke |
| < 13 | > 0.078 | extrem kurzwelliger Schwerpunkt der UVB-Strahlung: voraussichtlich sehr hohe Vitamin-D-Bestrahlungsstärke und extrem hohe Verbrennungs-Bestrahlungsstärke Typischer Messwert bei Lampen die mit Augenverbrennungen bei Reptilien assoziiert waren |
Literatur
763
[120] Kärhä, P. (2002). Calibration and intercomparison issues with broadband uv meters. UV News, 7, 29–34.
[119] Gugg-Helminger, A., Dähn, W., & Fenk, S. (2002). Manufacturer’s view on uv meters with different action spectra. UV News, 7, 20–28.
[38] Gugg-Helminger, A., Dähn, W., Fenk, S., & Angelo, B. 2004, October 1 Broadband and spectral measurement instrumentation for photobiological hazard evaluation. Unpublished paper presented at CIE Expert Symposium on Light and Health.
[112] Characterizing the performance of integral measuring uv-meters. (2000). UV News, 6, A-1–AA-36.
[668] Hoffmann, H., & Kirschner, A. (2010). Leserbrief. Elaphe N.F. 4, 76.
[678] Webb, A. R. (2000). Standardisation of data from ultraviolet radiation detectors. Radiation Protection Dosimetry, 91(1-3), 123–128.
[280] Larason, T. C. (2001). Avoiding errors in uv radiation measurements. Photonics Spectra,






Discussion